Heat Engines

Comments

Post a Comment

Popular posts from this blog

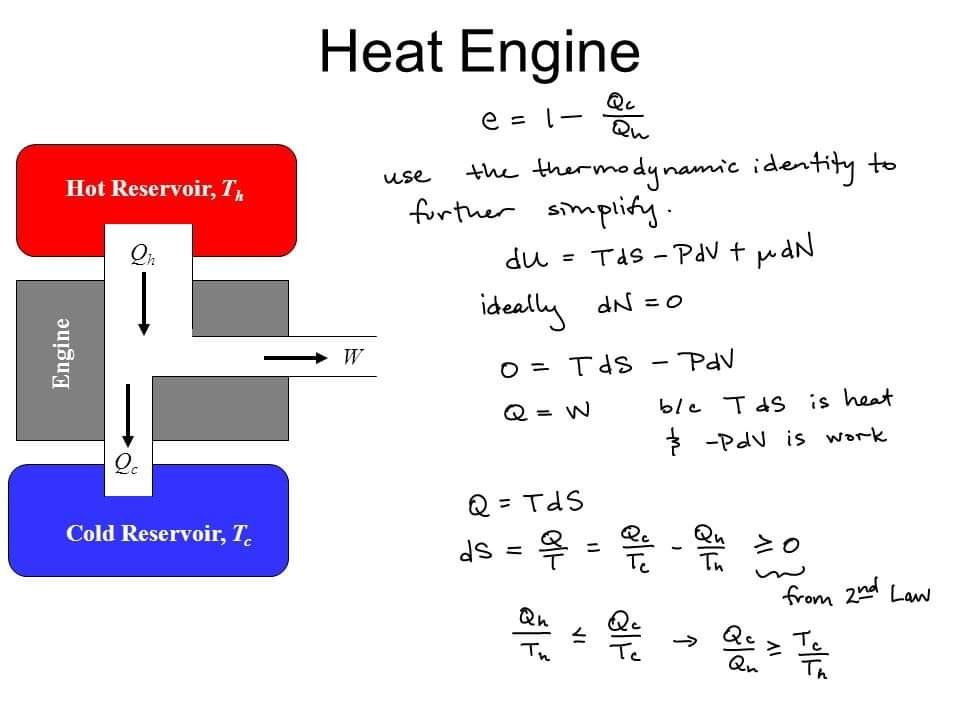
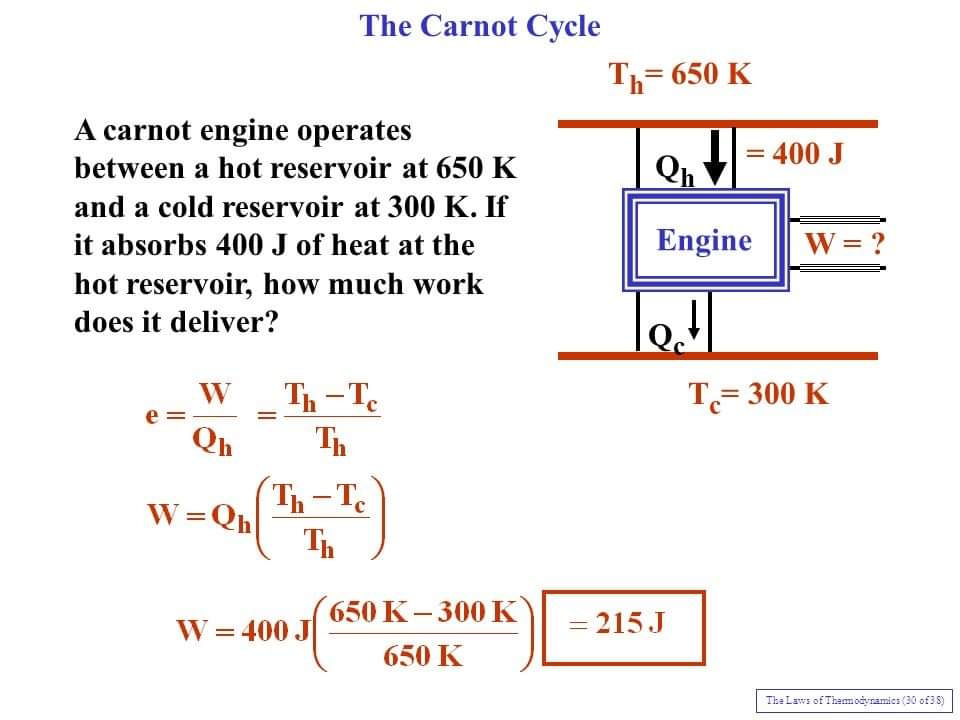
Impulse

Image
Q: Sensei ❓Is impulse a vector or scalar? Answer: Impulse is a vector, so a negative impulse means the net force is in the negative direction. 🔹Table of Contents: For better understanding, one should know the answer to the following questions. 1 What is impulse vs momentum? 2 What is impulse with example? 3 Is impulse a vector? 4 What is impulse write its formula? 5 What is called impulsive force? 6 Why is impulse equal to momentum? 7 What is the difference between impulse and force? 8 Why does impulse mean? 9 What is the formula and unit of impulse? 10 What is an example of impulse and momentum? 11 Is impulse a scalar force? 12 What is unit of velocity? 13 What is momentum unit? 14 How do you find impulse? 15 What are 3 examples of impulse? 16 Is impulse a physical quantity? 17 Does impulse increase with time? 18 Is velocity a vector? 19 Is momentum a force? 20 What is impulse of force give one example? 21 Which is an example of impulsive force? 22 Does a m...
Read more

Hands on demonstration for vectors

Image
Sheeba Nukrish Q: Under  learning by doing methodology can we teach the concept of vectors. Is there any hands-on demonstration that  can be done to make it simple.. 🍁 Solutions: Here's a hands-on demonstration that can make it simpler for learners: ▪️Co-ordinate system Materials needed: A ruler or meter stick A sheet of paper Pencil or pen Colored markers or highlighters Procedure: 1. Begin by explaining the basic idea of vectors. You can define a vector as a quantity that has both magnitude (size) and direction. 2. Draw a coordinate system on the sheet of paper with x and y axes labeled. You can use the ruler or meter stick to create straight lines for the axes. 3. Select a starting point (origin) on the coordinate system and mark it with a dot or an "O." 4. Choose a random point on the coordinate system and mark it with another dot. 5. Using the ruler or meter stick, draw an arrow from the origin to the random point, representing the vector. Explain...
Read more
Image
How do you know whether to use dot product or cross product in a vector problem? a. 1. The most basic difference is whether you are looking for a scalar result or a Vector result. Dot product gives you a scalar result whereas Cross product gives you a Vector result. 2. Basically the purpose of application differs. Dot product gives you an expression for Work done whereas Cross product gives you an expression for Torque. 3. Dot product would have been maximum if both the vectors had acted in the same direction, but a Cross product = 0 if both the vectors are in the same direction. More detailed explanation is given below- A. Dot product is simply the effect of one vector on the other should it be acting in the same direction as the base vector. Assume two vectors acting on a mass in the exact opposite directions. They would nullify each other. But if they were acting on the body in the same direction, the effect of the forces would be maximum. Assume vector a = 2i and vector b = 4i (bot...
Read more